How to enter a dynamic load in Diamonds?

You should know the variation in time of the dynamic load! After that you can define it in Diamonds and calculate the response.

Example

The rotating parts (100kN) of an arbitrary machine cause a harmonic load on a foundation slab. One cycle takes 4s. After each cycle the machine holds still for 1s, then the next cycle starts. The machine is supported in 4 positions.

Definition of the load

Make a dynamic load group

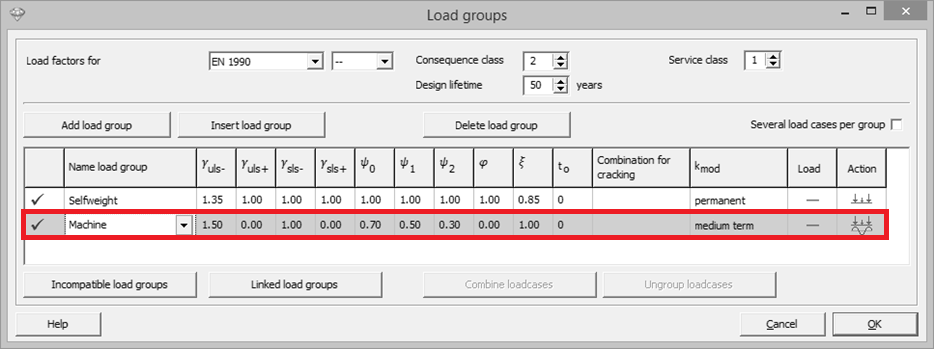
• Open the window ‘Loads Groups’ .
• Add a load group ‘Live load’.
• Set the ‘Action’ to   (click on  to change it to ).

Define the maximum value of the dynamic load as a static load

• The 100kN rotating mass translates into 4 point loads of 25kN. Define the 25kN as a static point load. In the next paragraph the time variation of these points load will be defined.

Define the properties of the wave

• Click on .
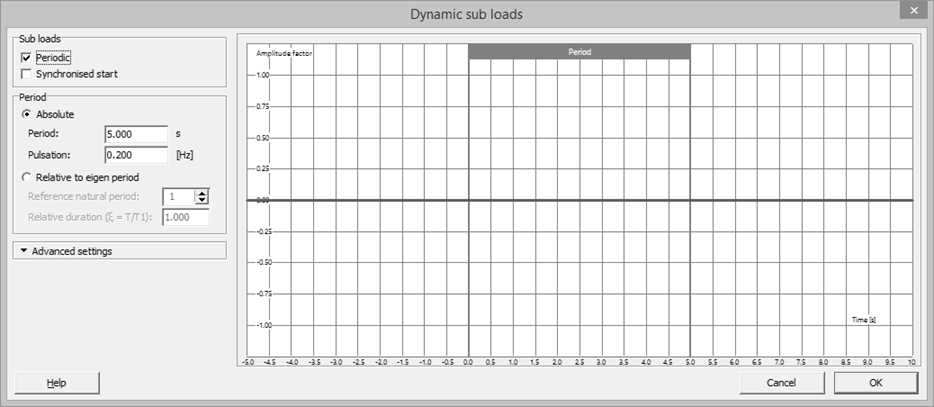
• Define the synchronization and the period.
  • Sub loads
    • When the machine is turned on, multiple cycles will be run. The wave is continuous, so ‘Periodic’ is checked.
    • ‘Synchronised start’ only applies if you have multiple sub load case always working together. Since that’s not the case here, we neglect this option.
  • The period is the length of one cycle, in this case 5s.
  • Advanced settings: leave everything on default. see reference manual.

Define the properties of one cycle

• Click on .
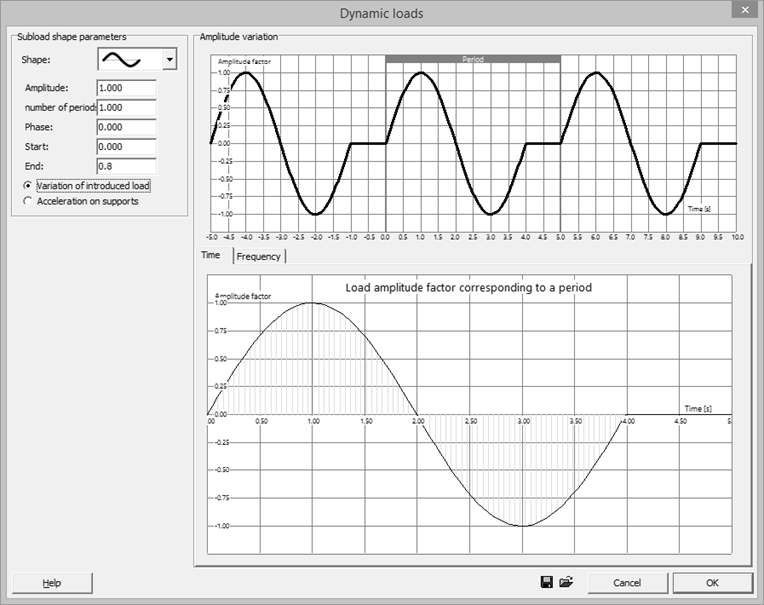
  • For the shape a sinus (harmonic wave) is chosen.
  • The amplitude factor is the multiplication factor (from -1 until 1) for the static load. Since the static load has the maximum value of the load +1 applies here.
  • One cycle is run in one period, so the number of periods equals 1.
  • Once the machine is turned on, the wave will start, so there’s no phase shift.
  • With ‘Start’/’End’ the start-/ endpoint of the wave can be delayed. You must enter a value (0 to 1) relative with respect to the period (start time = start * period). Since the wave from the machine is delayed between cycles, 0,8 is entered with ‘End’. 0,8 times 5s equals 4s (the length of one cycle), 0,2 times 5s equals 1s (the delay between the cycles).

Mass for modal analysis

To calculate the response of the structure, the modal parameters of the structure (eigen modes and – frequencies) must be known. The model parameters depend on the stiffness and mass distribution of thee structure.

• The stiffness is known by Diamonds because its in the geometry of the structure.
• The mass distibution is related to the vertical loads (point loads, line loads, surface loads) (0,981kN -> 100kg). The correlation coefficient φ multiplied by the combination factor Ψ₂ (for EN 1990) will determine the masses.

To define the masses:

• Open the window ‘Loads Groups’ .
• Set the correlation coefficient  φ to 1 for the self weight and the live load.

Calculate the response

Generate the combinations

• Click on the window ‘Loads Groups’ .
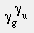• Click on the button .
• Select the required combinations and hit ‘OK’.

Run the analysis

• Click on the button or press ‘F9’ to start the analysis.
• The results can be viewed in the Results Configuration .